what size company could an earth-sized computer run?
A company with about 300 people (or rather, “variety”).
This is the result worked out in Stafford Beer’s Brain of the Firm (1972), brilliantly illustrating the complexity of real world decision making and absurdity of trying to “compute” decision making perfectly. It’s perhaps easiest to first follow the result of Bermermann’s limit, which establishes a theoretical upper bound on the rate of computation in matter. With this number (rounded by Beer), we arrive at the conclusion that a theoretically optimal computer with the mass of earth computing for the entire age of the earth (estimated by Beer at 1 billion years) could process (2 × 1047 bits/second/gram)·(π × 107 seconds/year)·(109 years)·(6 × 1027 grams) ≈ 1092 bits of information.
Next, we need to consider the “complexity” – or variety, as Beer & fellow cyberneticians call it – of a real world situation in bits. Variety is defined as the number of possible states. At this point, we’re interested in how a company – or “firm” – can respond to its environment. It follows that a firm has inputs (“receptors”) and outputs (“effectors”) connecting it to its environment (“situation”), and the variety of each must be at least as large as the variety of the environment. Let’s take a look at Brain of the Firm’s Figure 9:
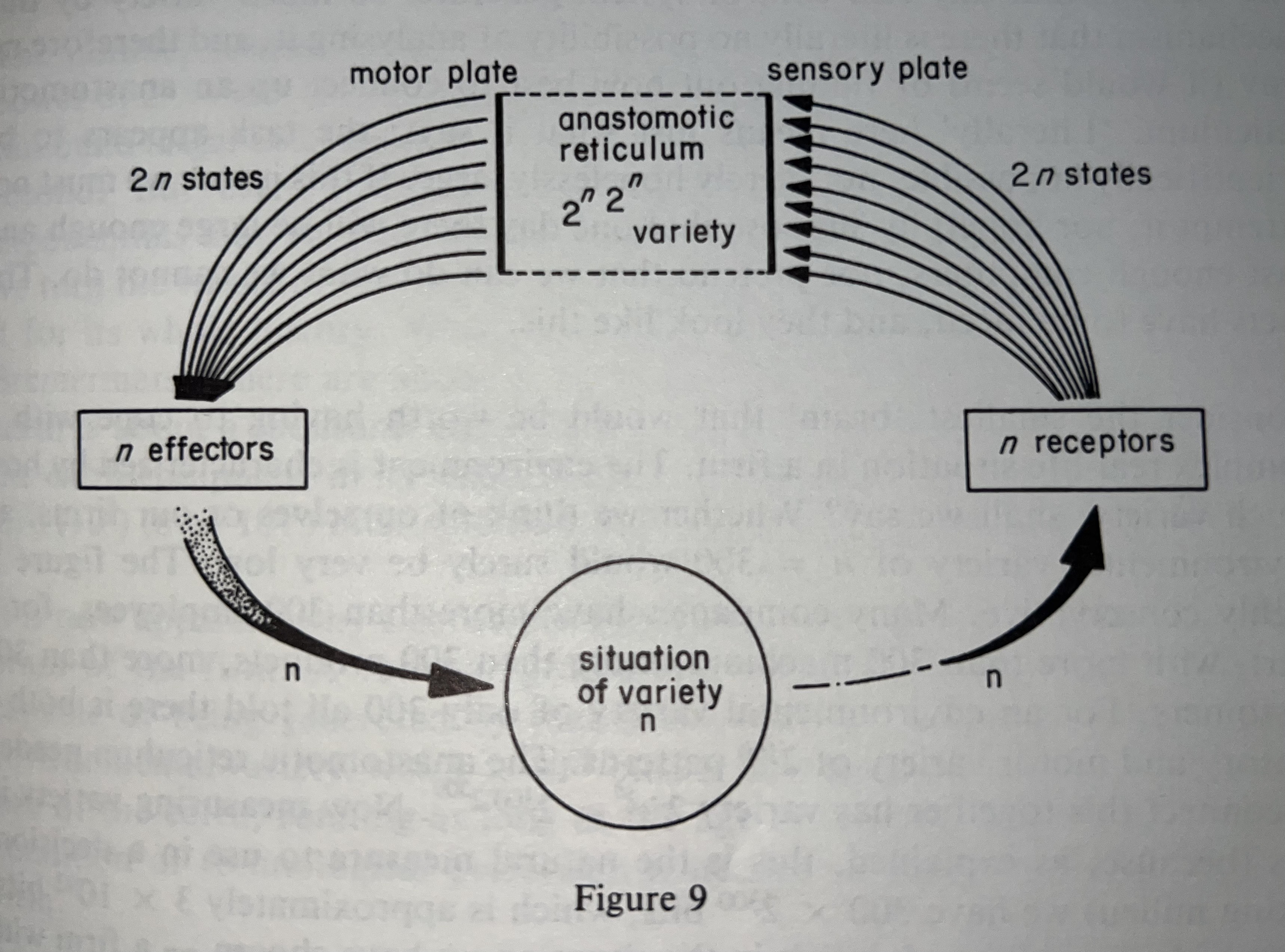
That is, for a firm with an environmental variety of 300, there must be 300 inputs and 300 outputs from the firm to match the environment. If each input receptor is either on or off, then the internal number states connecting to the firm is 2300 (note not to be confused by Figure 9 writing 2n as 2n in two places). Similarly on the output side, there are 300 possible outputs (each being on or off) mapping to 2300 internal states. The total variety of the firm is then 2300·2300 states, as the computational unit (i.e. “brain of the firm”, represented by the “anastomotic reticulum” in Figure 9) must be able to densely connect between all input and output states (why?), resulting in their multiplication together. Converting these internal states to representation via bits yields log2(2300·2300) = 300 × 2300 ≈ 3 × 1092 bits for a firm with environmental variety of 300 – and this is a very small amount of variety for any real world situation. It’s certainly an underestimate for a firm with 300 people. Looking back at the previous calculation, we see this is three times more than a theoretically optimal computer the mass of earth could compute in the entire age of the earth. Then again, if we estimated the age of the earth at 4.5 billion years, we have this 300 variety firm easily covered – at least for one situation in the real world, where time marches on and environments change.
Or, in Beer’s own words:
Consider the smallest ‘brain’ that would be worth having to cope with a complex real-life situation in a firm. The environment is characterized by how much variety, shall we say? Whether we think of ourselves or our firms, an environmental variety of n = 300 would surely be very low. The figure is highly conservative. Many companies have more than 300 employees, for a start, with more than 300 machines, more than 300 products, more than 300 customers. For an environmental variety of only 300 all told there is both a sensory and motor variety of 2300 patterns. The anastomotic reticulum needed to connect this together has variety 2n·2n = 2300·2300. Now measuring variety in bits (because, as explained, this is the natural measure to use in a decision-taking milieu) we have 300 x 2300 bits, which is approximately 3 × 1092 bits. That is the uncertainty implicit in the situation we have chosen – a firm with no more than 300 inputs and outputs, each of which has no more than two states.
The next part of the argument comes from physics, and is due to H.J. Bremermann (see Bibliography). According to quantum mechanics, there is a lower limit for the accuracy with which energy can be measured. That is, there is a permanent and fundamental degree of uncertainty in matter. Any attempt to improve the accuracy of one relevant measure will, according to Heisenberg’s Uncertainty Principle, perforce drive accuracy out of an associated measurement. The quantities involved are very small, but they turn out to matter very much. What Bremermann did was to apply the quantum law to one gram of matter for one second, and to show the lower limit for accurate measurement places an upper limit on the information-processing capacity of the material. Beyond that limit, noughts will become confused with ones, and computations must become ambiguous. In one second, he concludes, this gram of typical matter cannot cope with more than 2 × 1047 bits of data. Of course, no one has a gram of anything which can actually be used to compute so great an amount of data; microminiaturization has not advanced that far. But, and this is his point, even at the end of technological road it would be impossible to cram more than 2 × 1047 bits into a gram of matter in one second – because bits would be confused by Heisenbergian uncertainty. Bremermann has conjectured, with this argument, the requisite variety of matter itself.
The numbers sound large; indeed, we have just been studying the explosive power of 2n – and here n is followed by forty-seven noughts. Moreover, we can build larger computers than a gram weight, and use them for longer than a second. But even people who are accustomed to thinking in terms of exponentials may be taken aback by the next stage of the argument. Suppose we turn the whole of this earth, the terrestrial globe, into a computer, and run it for its whole history. What variety has this fantastical machine? Well, says Bremermann, there are about π × 107 seconds in a year, and the age of the earth is about a thousand million years. Its mass is about 6 × 1027 grams. So the earth-computer, in its whole history, could have handled (2 × 1047) (π × 107) (109 years) (6 × 1027 grams) bits. And that works out at something like 1092 bits.
It is now apparently why I chose the variety n = 300 for my example about the brain of the firm. A few paragraphs ago we saw that the reticular variety capable of being generated by that brain, with its conservative estimate of environmental variety, was 3 × 1092 bits. It now turns out that a computer the size of the earth, running as long as the age of the earth and in the ultimate condition of technological perfection is needed to do the sums for this tiny firm.